Twitter(現X)で面白い算数の問題に出会ったのでメモします。
タイトルの通りですが、小1の算数の問題で、僕が即答できなかった問題があるので共有します。
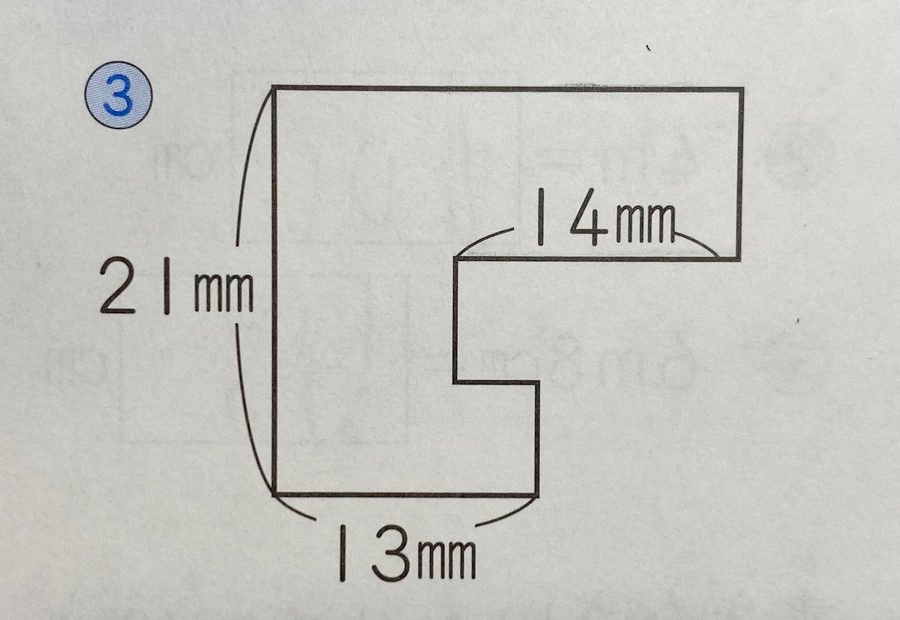
こんな図形で、「この図形の外周の和を求めなさい」という問題でした。
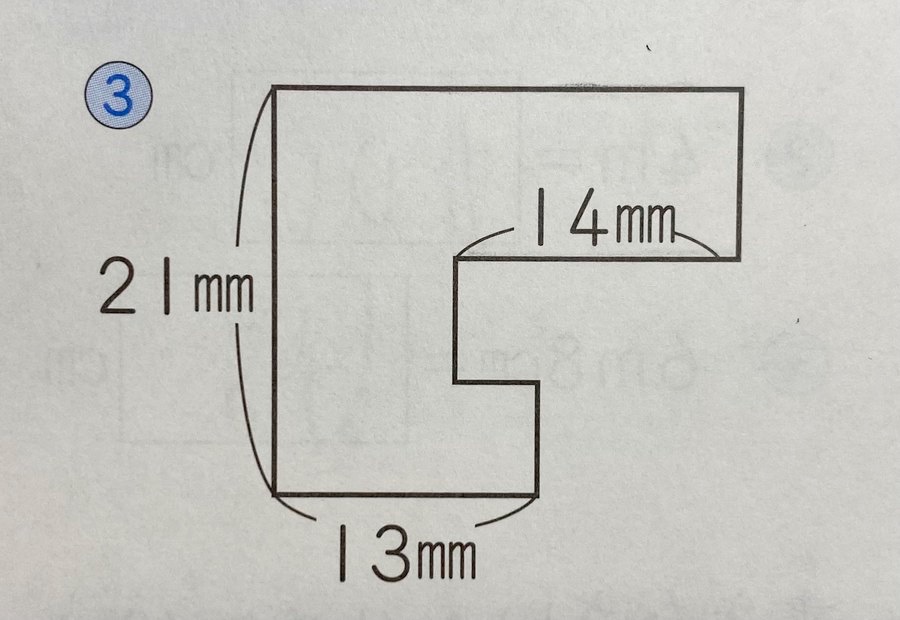
これ、僕、即答できないで反射的にTwitter有識者に質問を投げ、返答が返ってくる前に答えに辿り着きました。
この問題、上辺が不定に見える事で、実際不定なんですが、僕の考えた方法を含め3つの答えの出し方あります。
基本的には全部同じ事を言っているのですが、3つ説明していきます。
不定の外周と差分を図る方法
まず共通として、左下を始点とする場合上移動は21mm、下への戻りも分割されているだけで合計21mmです。
その上で、横線について、上辺をA、左に戻る14mmをB、右に折り返す差分をC、左に戻る13mmをDとします。
この場合、Aは不定なんですが、Aを動かすと、右に折り返す差分Cも同時に動きます。
なので、計算としてはA+C=B+Dで、B+Dはどっちも数字が出ているので27mmです。よってA+Cも27mmです。
なので、結局外周は21mm+21mm+27mm+27mmで、答えは96mmです。
僕はこの方法で答えに至りました。
Xを置く方法
人からご指摘頂いた方法の1つとして、次があります。
縦線については21mmの行きと21mmの帰りは一緒です。
横線について、上辺をA、左に戻る14mmをB、右に折り返す差分をC、左に戻る13mmをDとします。
この場合、Cの長さをXとすると、こういう計算ができます。
- Cの長さはX
- 上辺の長さ(A)は14+13-X
- 上辺以外の横の長さ(B+C+D)は14+13+X
よって横移動の量は(14+13-X)+(14+13+X)。計算するとXが消滅し、横移動の同型は54mm。
縦移動の合計が21+21で42なので、足して96mmです。
Xの置き方で解決ができます。
外周の合計はシンプルにベクトルで計算できる方法
もう一つご指摘頂いたのはこれです。
まず図形を考えるに当たり、左下から移動して左下に戻ってくるには、「同じだけ上と下の距離を移動し」「同じだけ左右の距離を移動する」結果でないと図形が完成しません。
なのでシンプルに考えると、こうなります。
- 上への移動は21mm
- 下への移動は21mmでないと図形が完成しない
- 右への移動はBとDで27mm
- 左への移動は27mmでないと図形が完成しない
よって移動距離は21mm+21mm+27mm+27mmで96mmです。
これ、とてもシンプルですよね。
というわけで3つの解凍方法が出ました。
というわけで、この問題、不定の長さを含むのですが、問題の整理で3つの回答方法が出ました。
ただ、結局行っているのは、全部最後の方法の「行った分だけ戻らないと図形が完成しない」前提なんですよね。
これを小1でやるのは相当冴えていると言うか、かなり柔軟な頭じゃないと厳しい気がします。
なお、個人的に調べたんですが、そもそも「mm」っていう単位は小学2年制で習う範囲のはずなので(もしかして学習指導要綱の改定で変わっているかも知れません)、この問題って本来小1でやるレベルじゃないと思うんですよね……。
僕の見立てが外れていなければ、これ、恐らく公立じゃなく私立の問題だと思うのですが、このレベルの問題を小1で「当たり前」にできているのだとしたら。僕の小学1年生の時代に比べて圧倒的に加速度がついて時代が進んでいるという事なので、結構怖い気がします……。
というわけで、Twitter(現X)で面白い問題を見つけて解いたのでせっかくなので共有しましたー。
この記事を書いた人 Wrote this article
如月翔也
ガジェットとAppleとTRPGが大好きな中年男です。文章をとにかく書くのが好きなので毎日のように色々なブログで文章を打ちまくっています。もし何か心に引っかかるものがあれば私のTwitterをフォローして頂けると更新情報が流れます。